Calculating Pressure Drop of Nanofiber Air Filter Media

Nanofibers are becoming an integral part of many advanced air filtration media thanks to their enormous specific surface area. The large surface area, however, can cause strong resistance against fluid motion, which leads to an increase in pressure drop. Pressure drop caused by fibrous media has been the focus of many pioneering studies in the past, resulting in analytical or empirical correlations such as that developed by Davies (1973). However, such correlations are inaccurate in predicting the pressure drop of fibrous media made up of nanofibers. This is because these expressions/correlations do not take into account the effects of aerodynamic slip on nanofibers. Aerodynamic slip takes place when the diameter of the fibers is comparable to the mean free path of the molecules in the air (about 64 nm in normal temperatures and pressures), and the flow field around the fiber can no longer be assumed a continuum.

The 2-D analytical work of Kuwabara (1959) has long been used for predicting the pressure drop across fibrous filters. The work of Kuwabara (1959) has later been modified to include the effects of aerodynamic slip (Brown 1993). However, the problem with the modified Kuwabara model, as well as all other expressions developed using a 2-D representation of the fibrous filters with fibers arranged in ordered configurations, is that they overestimate the pressure drop of real fibrous media.

In this concern, we have developed an expression, which does not have the above-mentioned limitations, i.e., it is not limited to large fibers, like the Davies correlation, and also does not overestimate the pressure drop like the above 2-D models. Our expression is, in fact, a correction factor added to the empirical correlation of Davies.

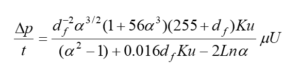
where is called the Kuwabara hydrodynamic factor. In this expression,and  are the air pressure (in Pa), velocity (in m/s), and viscosity (in Pa.s), whereas (in m), , and (in nm) are filter thickness, solid volume fraction, and fiber diameter, respectively.

Unlike any previous correlations, this expression is accurate for both microfibers and nanofibers. The accuracy of this expression is examined using series of realistic 3-D numerical simulations. Readers are referred to the work of Hosseini and Tafreshi (2010) for more information.

References

Davies, C.N., 1973. Air Filtration. Academic Press, London.

Kuwabara, S., 1959. The Forces Experienced by Randomly Distributed Parallel Circular Cylinders of Spheres in a Viscous Flow at Small Reynolds Number. Journal of the Physical Society of Japan 14 (4), 527.

Brown, R.C., 1993. Air Filtration. Pergamon Press.

Hosseini, S.A, and Tafreshi, H.V., 2010. Modeling Permeability of 3-D Nanofiber Media in Slip Flow Regime. Chemical Engineering Science, 65, 2249.