About the Dewatering of Porous Structures or Packed Beds by Mechanical Means

To understand the deliquoring process of packed beds, it is important to know the various fluid components and their binding mechanisms present in a saturated packed bed. Not every portion of liquid can be removed by mechanical means. Figure 1 shows a group of individual particles with typical liquid distribution.
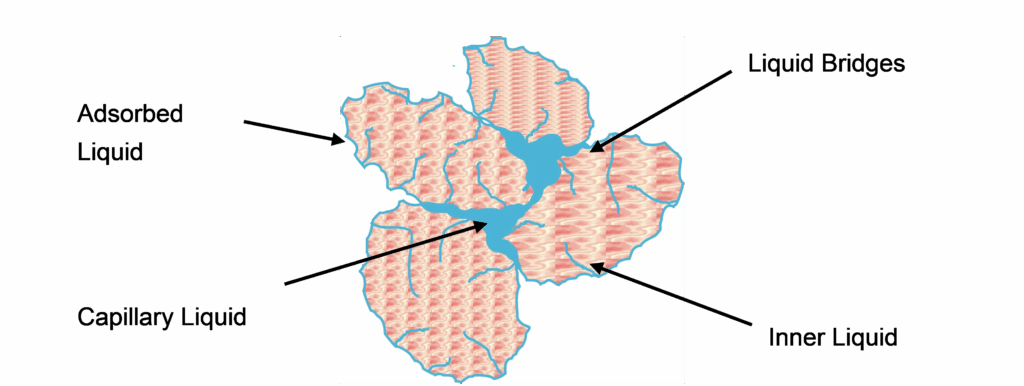
At the beginning of deliquoring, the relatively easily movable capillary liquid is pushed out of the open pores. The effectiveness of this process depends, among other things, on the pore size distribution. It is not uniform; hence there are already empty pores while others are still filled. In for instance a filter cake the pore system is understood to be hydraulically interconnected channels of various diameters and lengths that are networked with each other in all directions.
The determination of pore size distribution cannot be estimated based on product data, such as Particle diameter with the assumption of uniform random packing. Segregation and agglomeration cause local anisotropies that disrupt the cake structure. The characterization of a bulk material is done in practice by determining a hydraulic pore diameter. Under the assumption of size-distributed, parallel, cylindrical pore channels a flow test with predetermined pressure intervals leads to the pore size distribution.
The hydraulic diameter according to Eq. 1 is the equivalent diameter of a cylinder, which equals the volume of a pore with arbitrary shape. A is area and U circumference.

Based on the assumption of cylindrical pore channels, the flow within the pore can be assumed to be a plug flow according to Hagen-Poiseuille. Therefore the pressure loss hK over the channel length can be determined as:
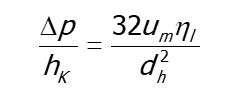
The average superficial velocity u can be calculated using the Darcy equation. The mean absolute velocity follows from equation 4.
eq. 3
eq. 4
The geometrical characteristics of the packed bed are accounted for by the specific flow resistance rc. With eq. 2 – eq. 4 this yields the mean hydraulic diameter.
eq. 5
In contrast to the single-phase flow during e.g. cake formation, during deliquoring or under-saturation interfacial tension effects need to be considered. Between two immiscible fluids an interface is formed. To increase the interfacial area energy is required. This energy is called interfacial or surface tension gL. The interfacial tension compensates the pressure difference in the two phases. This results in a curved boundary. The pressure difference is called the capillary pressure. By convention it is established that the capillary pressure is pK>0, when the denser phase has an over pressure and pK<0 when the in the denser phase has a under pressure.
Applied to a pore with solid walls (three phase), this means the effective capillary pressure at the interface between liquid and gas needs to be overcome by an externally applied potential (e.g. pressure gradient, centrifugal force etc.). This can also be explained by a force balance according to Figure 2.
Figure 2 : Force balance around interface
For a wetting liquid (d <90 °), which has not yet reached the capillary equilibrium height, due to surface tension it results a gravity opposing force which leads to an increase in liquid level up to the capillary equilibrium height hK. In the equilibrium state, lift weight of the liquid column and capillary force equal exactly. The angle formed between the vessel wall and the liquid is called wetting angle d. By convention pL<pG leads to a positive capillary pressure pK.
For a non-wetting liquid (d> 90 °) a negative capillary pressure results, i.e. the capillary is emptying without pressure gradient. At (d = 90 °) the capillary pressure pK equals 0.
For a spherical boundary under consideration of the capillary radius r the force balance results in most common form of the Laplace equation.
eq. 6
With increasing pore radius the capillary pressure of a wetting liquid and thus the capillary rise is smaller.
It follows that when applying a pressure differential, the first large capillaries are drained and those whose capillary pressure pK£Dp. Characteristic for the deliquoring is the occurrence of so-called “fingering”, i.e. a premature drainage of larger pores compared to plug flow. After emptying the largest pore a gas breakthrough occurs and hence the collapse of the driving pressure difference. In centrifugal dewatering this does not occur. Further deliquoring can be realized only by enormous compressor performance. Depending on the external pressure difference and the pore size distribution therefore only a proportion, namely from the pores with pK£Dp, of liquid can be removed.
Liquid bridges, adsorbed or adhesive liquid and inner liquid are difficult to access with gas pressure difference. By means of capillary pressure, it is possible to make predictions about the dewaterability of a product, but not the kinetics of moisture removal.
All of the above is also transferable to the processes carried out during pore size distribution measurement by for instance a PMI type instrument.
Author
Mathias Stolarski
DuPont
AFS 2nd Vice Chair
| Since Dec. 2008 | Research Engineer, DuET-Particle Technology-Separations DuPont Experimental Station, Wilmington, USA Key Projects: BioFuels – Downstream Processing Bioseparation Dynamic Cross-Flow Filtration, Membrane Separation Upstream – Downstream Process Interaction |
| Jun. 2004 – Nov. 2008 | Research Assistant at the Institute of Mechanical Process Engineering and Mechanics, University of Karlsruhe Process Engines Group Key Projects: Magnetic centrifugation Magnetic filtration Solid Liquid Separation |