Surface Wettability Affects Filtration

Wettability is a property that exists on every surface and influences the behavior of a fluid surrounding the surface due to the intermolecular interactions in either attractive or repelling form. Surface wettability is determined by the balance between the adhesive and cohesive forces at the surface interfaces. There are lots of examples in nature that illustrate the presence of wettability; such as, water drops on a lotus leaf, water drops found on the car windshield, water drops found on a spider web and many more. In filtration, liquid droplets or solid particles have a certain degree of affinity to the filtration media which influences its loading or saturation properties. In the case of solid or dust particles depositing on a fiber or a substrate surrounded by continuous gas and discontinuous liquid phases, the loading is dominated by the adhesion and drag forces. The liquid droplets react differently when captured by the substrate and their shape is a function of the molecular interactions at three different interfaces (solid-liquid-air) as in the case of air filtration given by Young’s equation.
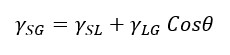
Here γSG is the surface tension at the solid-gas interface; γSL is the surface tension at the solid-liquid interface and γLG is the surface tension at the liquid-gas interface. In the equation γSL can be determined using pure liquids with their dispersive and attractive components and the contact angle with respect to each liquid.
During the separation of two fluid streams with a continuous and a dispersed phase (ex. hydrocarbon oils-gas) using a fibrous coalescer media, the wettability of liquid drops on the media surface influences filtration performance. In the case of air filtration, like crankcase ventilation requirements, the droplets are captured by the substrate due to filtration mechanisms determined by the velocity regimes. After capture however, the growth, coalescence and drainage of liquid drops is highly dependent on surface wettability along with other flow parameters. Analytical modeling to predict the dynamic behavior in coalescence process is an ongoing endeavor with some work available for steady state conditions. One example of such a simplified analytical model is the one proposed by Liew and Conder, which is used to estimate pressure drop for a fibrous filter media under steady state conditions with constraints on packing density αf between 7.6% and 14% and fiber diameter df between 4 and 22 μm. Another example is the empirical correlation developed by the author and Chase to predict the drag coefficient of liquid drops on single fiber (where Re= Reynolds number and Ca=Capillary number).


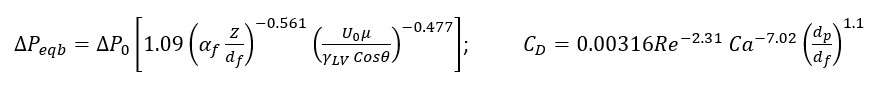
Characterization of surface wettability is also important for filter media design since it affects filtration performance. Fibrous mat wettability can be characterized by contact angle measurements using either the pendant drop or sessile drop method for static and dynamic conditions. The wettability of the fibers and fiber mat affects the motion of liquid drops before and after coalescence, and, therefore, the effective drainage of collected liquid. Improved drainage helps maintain a low pressure drop and high efficiency for a particular droplet size.